统计

一、概率

1.古典概型

2.贝叶斯统计

3.组合概率

二、分布

1.正态分布

2.几何分布

3.泊松分布

4.期望计算方法

5.抽样分布：卡方、F、T

6.相关性检验

7.峰度、偏度、统计量

三、假设检验

1.P值

2.第一类错误、第二类错误

3.原假设、备择假设

4.参数估计：最大似然估计、无偏估计、区间估计

5.T检验和Z检验

6.有效样本量计算

7.辛普森悖论

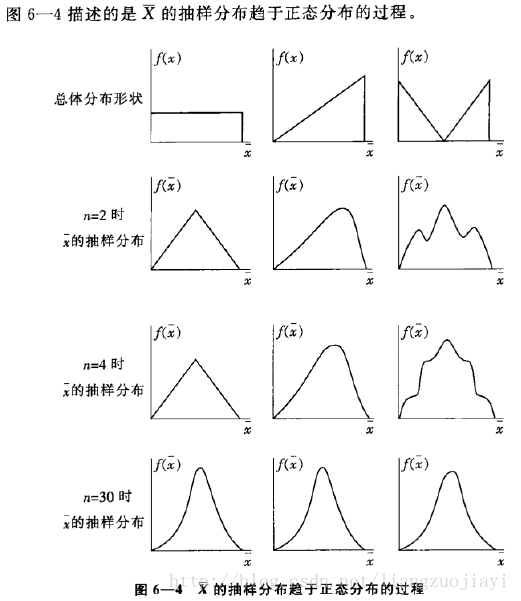
8.中心极限定理

中心思想是无论是什么分布的数据，当我们从中抽取相互独立的随机样本，且采集的样本足够多时，样本均值的分布将收敛于正态分布。

img
img

9.ABtest

10.因果推断

11.贝叶斯？

四、其他

1.概率和似然

概率是在特定环境下某件事情发生的可能性，也就是结果没有产生之前依据环境所对应的参数来预测某件事情发生的可能性。

根据参数求结果的可能性

似然刚好相反，是在确定的结果下去推测产生这个结果的可能环境（参数）

根据结果求参数的可能性

2.两个向量之间的相似性计算有什么方法

距离的性质：非负、同一、对称、三角不等式

曼哈顿距离，欧氏距离，余弦相似度，字符串距离、汉明距离

3.皮尔森相关系数以及如何解读，相关、独立、线性相关区别

简单相关系数/皮尔森相关系数：用来度量两个变量间的线性相关程度 \[ r(X,Y)=\frac{Cov(X,Y)}{\sqrt{Var[X]Var[Y]}} \] =0:无关，-：负相关，+：正相关

相关：（？）

独立：\(p(x,y)=p_1(x)*p_2(y)\)

4.完整解释PCA， PCA缺点：高维数据能适用PCA吗？类别变量one-hot能用PCA吗？

image-20230213143219185

image-20230213143202769

将离散型特征使用one-hot编码，会让特征之间的距离计算更加合理。

5.偏态分布怎么处理？

但是现实生活中总是会存在不是正态分布的情况，非正态分布，那就是偏态分布了，有两种，左偏（负偏态）和右偏（正偏态），可以用偏度来描述，偏度>0，则频数分布的高峰向左偏移，呈右（正）偏态分布；偏度<0，则频数分布的高峰向右偏移，呈左（负）偏态分布；|偏度|>1，呈高度偏态，0.5<|偏度|<1，呈中等偏态。

对于偏态分布的数据，我们需要做一些处理使其变换为正态分布，常用的变换方式有

  1. 对数变换：适用于相乘关系的数据、高度偏态的数据
  2. 平方根变换：适用于泊松分布（方差与均数近似相等）的数据、轻度偏态的数据
  3. 反正弦变换：适用于百分比的数据、中度偏态的数据
  4. 倒数变换1/x：适用于两端波动较大的数据